小学六年级数学数的认识知识点归纳及公式全部人教版资料整理

对于学生而言，通过对数学知识点的归纳总结，能够帮助他们建立起全面系统的数学概念和思维方式。这有助于学生更好地掌握和运用数学知识，提高他们解决实际问题的能力。下面是小编整理的小学六年级数学数的认识知识点归纳，仅供大家参考。

文章目录

小学六年级数学数的认识知识点归纳

六年级数学公式全部人教版

六年级数学路程问题应用题及答案

六年级数学相遇问题解题技巧

六年级数学必考难题带答案

小学六年级数学数的认识知识点归纳

一、 数与代数

▲ 数的认识

● 整数

1、整数的意义：自然数和0都是整数。

2、自然数：我们在数物体的时候，用来表示物体个数的1，2，3……叫做自然数。

　　一个物体也没有，用0表示。 0是最小的自然数。

3、计数单位：一（个）、十、百、千、万、十万、百万、千万、亿……都是计数单位。

　　每相邻两个计数单位之间的进率都是10。这样的计数法叫做十进制计数法。

4、数位：计数单位按照一定的顺序排列起来，它们所占的位置叫做数位。

5、数的整除：

　（1）整除、倍数、约数：整数a除以整数b(b ≠ 0），除得的商是整数而没有余数，我们就说a能被b整除，或者说b能整除a 。

　　如果数a能被数b（b ≠ 0）整除，a就叫做b的倍数，b就叫做a的约数（或a的因数）。倍数和约数是相互依存的。例如因为35能被7整除，所以35是7的倍数，7是35的约数。

　　一个数的约数的个数是有限的，其中最小的约数是1，最大的约数是它本身。例如：10的约数有1、 2、5、10，其中最小的约数是1，最大的约数是10。

　　一个数的倍数的个数是无限的，其中最小的倍数是它本身。3的倍数有：3、6、9、12……其中最小的倍数是3 ，没有最大的倍数。

　（2） 能被2、3、5整除的数的特征：

能被2整除的数：个位上是0、2、4、6、8的数

能被3整除的数：各位上数字的和能被3整除.

能被5整除的数：个位上是“0”或是“5”的数。

　　 （3）奇偶性：能被2整除的数叫做偶数。 不能被2整除的数叫做奇数。

　 　0也是偶数。自然数按能否被2 整除的特征可分为奇数和偶数。

　　 （4）质数与合数：一个数，如果只有1和它本身两个约数，这样的数叫做质数（或素数），

100以内的质数有：2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、 59、61、67、71、73、79、83、89、97。

一个数，如果除了1和它本身还有别的约数，这样的数叫做合数，

例如4、6、8、9、12都是合 数。

　　 1不是质数也不是合数，非0自然数除了1外，不是质数就是合数。如果把非0自然数按其约数的个数的不同分类，可分为质数、合数和1。

（5）分解质因数：每个合数都可以写成几个质数相乘的形式。其中每个质数都是这个合数的因数，叫做这个合数的质因数，例如15=3×5，3和5叫做15的质因数。把一个合数用质因数相乘的形式表示出来，叫做分解质因数。例如把28分解质因数28=22×7

　（6）公约数与公倍数：几个数公有的约数，叫做这几个数的公约数。其中最大的一个，叫做这几个数的最大公约数，例如12的约数有1、2、3、4、6、12；18的约数有1、2、3、6、9、18。其中，1、2、3、6是12和1 8的公约数，6是它们的最大公约数。

　 　公约数只有1的两个数，叫做互质数，成互质关系的两个数，有下列几种情况：

　　 * 1和任何自然数互质。 * 相邻的两个自然数互质。

　　 * 两个不同的质数互质。 * 当合数不是质数的倍数时，这个合数和这个质数互质。

　　 两个合数的公约数只有1时，这两个合数互质，如果几个数中任意两个都互质，就说这几个数两两互质。

　　如果较小数是较大数的约数，那么较小数就是这两个数的最大公约数。

　　如果两个数是互质数，它们的最大公约数就是1。

　　几个数公有的倍数，叫做这几个数的公倍数，其中最小的一个，叫做这几个数的最小公倍数，如2的倍数有2、4、6 、8、10、12、14、16、18 ……，3的倍数有3、6、9、12、15、18 ……， 其中6、12、18……是2、3的公倍数，6是它们的最小公倍数。。

　　 如果较大数是较小数的倍数，那么较大数就是这两个数的最小公倍数。

　 　 如果两个数是互质数，那么这两个数的积就是它们的最小公倍数。

　　 几个数的公约数的个数是有限的，而几个数的公倍数的个数是无限的。

● 小数

1、小数的意义

　　把整数1平均分成10份、100份、1000份…… 表示这样的的十分之几、百分之几、千分之几…… 的数可以用小数表示。

　　一位小数表示十分之几，两位小数表示百分之几，三位小数表示千分之几……

小数点左边的数叫做整数部分，小数点右边的数叫做小数部分。

　　在小数里，每相邻两个计数单位之间的进率都是10。小数部分的最高分数单位“十分之一”和整数部分的最低单位“一”之间的进率也是10。

　　2、小数的分类

　　纯小数：整数部分是零的小数，叫做纯小数。例如： 0.25 、 0.368 都是纯小数。

　　带小数：整数部分不是零的小数，叫做带小数。 例如： 3.25 、 5.26 都是带小数。

　　有限小数：小数部分的数位是有限的小数，叫做有限小数。 例如：41.7 、 25.3 、 0.23 都是有限小数。

　　无限小数：小数部分的数位是无限的小数，叫做无限小数。 例如： 4.33 …… 3.1415926 ……

　　无限不循环小数：一个数的小数部分，数字排列无规律且位数无限，这样的小数叫做无限不循环小数。 例如：∏

　　循环小数：一个数的小数部分，有一个数字或者几个数字依次不断重复出现，这个数叫做循环小数。 例如： 3.555 …… 0.0333 …… 12.109109 ……

　　一个循环小数的小数部分，依次不断重复出现的数字叫做这个循环小数的循环节。 例如： 3.99 ……的循环节是“ 9 ” ， 0.5454 ……的循环节是“ 54 ” 。

　　纯循环小数：循环节从小数部分第一位开始的，叫做纯循环小数。 例如： 3.111 …… 0.5656 ……

　　混循环小数：循环节不是从小数部分第一位开始的，叫做混循环小数。 3.1222 …… 0.03333 ……

　　写循环小数的时候，为了简便，小数的循环部分只需写出一个循环节，并在这个循环节的首、末位数字上各点一个圆点。如果循环 节只有 一个数字，就只在它的上面点一个点。例如： 3.777 …… 简写作————- 0.5302302 …… 简写作———-。

● 分数

　　1、分数的意义

　　把单位“1”平均分成若干份，表示这样的一份或者几份的数叫做分数。

　　在分数里，中间的横线叫做分数线；分数线下面的数，叫做分母，表示把单位“1” 平均分成多少份；分数线下面的数叫做分子，表示有这样的多少份。

　　把单位“1”平均分成若干份，表示其中的一份的数，叫做分数单位。

　　2、分数的分类

　　真分数：分子比分母小的分数叫做真分数。真分数小于1。

　　假分数：分子比分母大或者分子和分母相等的分数，叫做假分数。假分数大于或等于1。

　　带分数：假分数可以写成整数与真分数合成的数，通常叫做带分数。

　　3、约分和通分　把一个分数化成同它相等但是分子、分母都比较小的分数，叫做约分。

　　分子分母是互质数的分数，叫做最简分数。

　　把异分母分数分别化成和原来分数相等的同分母分数，叫做通分。

● 百分数

　1、百分数的意义：表示一个数是另一个数的百分之几的数 叫做百分数,也叫做百分率 或百分比。

▲ 数的读、写法

　　1、整数的读法：从高位到低位，一级一级地读。读亿级、万级时，先按照个级的读法去读，再在后面加一个“亿”或“万”字。每一级末尾的0都不读出来，其它数位连续有几个0都只读一个零。

　　2、整数的写法：从高位到低位，一级一级地写，哪一个数位上一个单位也没有，就在那个数位上写0。

　　3、小数的读法：读小数的时候，整数部分按照整数的读法读，小数点读作“点”，小数部分从左向右顺次读出每一位数位上的数字。

　　4、小数的写法：写小数的时候，整数部分按照整数的写法来写，小数点写在个位右下角，小数部分顺次写出每一个数位上的数字。

▲ 数的改写

一个较大的多位数，为了读写方便，常常把它改写成用 “万”或“亿”作单位的数。有时还可以根据需要，省略这个数某一位后面的数，写成近似数。

　　1、准确数：在实际生活中，为了计数的简便，可以把一个较大的数改写成以万或亿为单位的数。改写后的数是原数的准确数。 例如把 1254300000 改写成以万做单位的数是 125430 万；改写成 以亿做单位 的数 12.543 亿。

　　2、近似数：根据实际需要，我们还可以把一个较大的数，省略某一位后面的尾数，用一个近似数来表示。 例如： 1302490015 省略亿后面的尾数是 13 亿。

　　3、取近似数的方法：

⊙四舍五入法：要省略的尾数的最高位上的数是4 或者比4小，就把尾数去掉；如果尾数的最高位上的数是5或者比5大，就把尾数舍去，并向它的前一位进1。例如：省略 345900 万后面的尾数约是 35 万。省略 4725097420 亿后面的尾数约是 47 亿。

⊙　进一法：实际中，使用的材料都要比计算的结果多一些 ，因此，要保留近似数的时候，省略的位上是4或者比4小，都要向前一位进1。这种取近似值的方法叫做进一法。

⊙去尾法：

　4、大小比较

　　（1）比较整数大小：比较整数的大小，位数多的那个数就大，如果位数相同，就看最高位，最高位上的数大，那个数就大；最高位上的数相同，就看下一位，哪一位上的数大那个数就大。

　　（2）比较小数的大小：先看它们的整数部分，，整数部分大的那个数就大；整数部分相同的，十分位上的数大的那个数就大；十分位上的数也相同的，百分位上的数大的那个数就大……

　　（3）比较分数的大小:分母相同的分数，分子大的分数比较大；分子相同的数，分母小的分数大。分数的分母和分子都不相同的，先通分，再比较两个数的大小。

▲ 数的互化

　　1、小数化成分数：原来有几位小数，就在1的后面写几个零作分母，把原来的小数去掉小数点作分子，能约分的要约分。

　　2、分数化成小数：用分母去除分子。能除尽的就化成有限小数，有的不能除尽，不能化成有限小数的，一般保留三位小数。

　　3、一个最简分数，如果分母中除了2和5以外，不含有其他的质因数，这个分数就能化成有限小数；如果分母中含有2和5 以外的质因数，这个分数就不能化成有限小数。

　　4、小数化成百分数：只要把小数点向右移动两位，同时在后面添上百分号。

　 5、百分数化成小数：把百分数化成小数，只要把百分号去掉，同时把小数点向左移动两位。

　　6、分数化成百分数：通常先把分数化成小数（除不尽时，通常保留三位小数)，再把小数化成百分数。

　　7、百分数化成小数：先把百分数改写成分数，能约分的要约成最简分数。

▲ 数的整除

　　1、把一个合数分解质因数，通常用短除法。先用能整除这个合数的质数去除，一直除到商是质数为止，再把除数和商写成连乘的形式。

　　2、求几个数的最大公约数的方法是：先用这几个数的公约数连续去除，一直除到所得的商只有公约数1为止，然后把所有的除数连乘求积，这个积就是这几个数的的最大公约数 。

　　3、求几个数的最小公倍数的方法是：先用这几个数（或其中的部分数）的公约数去除，一直除到互质（或两两互质）为止，然后把所有的除数和商连乘求积，这个积就是这几个数的最小公倍数。

　　4、成为互质关系的两个数：1和任何自然数互质 ； 相邻的两个自然数互质； 当合数不是质数的倍数时，这个合数和这个质数互质； 两个合数的公约数只有1时，这两个合数互质。

▲ 约分和通分

　　1、约分的方法：用分子和分母的公约数（1除外）去除分子、分母；通常要除到得出最简分数为止。

　　2、通分的方法：先求出原来的几个分数分母的最小公倍数，然后把各分数化成用这个最小公倍数作分母的分数。

▲ 数的性质和规律

　　（一）商不变的规律

　　商不变的规律：在除法里，被除数和除数同时扩大或者同时缩小相同的倍，商不变。　　 （二）小数的性质 小数的性质：在小数的末尾添上零或者去掉零小数的大小不变。

　　（三）小数点位置的移动引起小数大小的变化

　　1、小数点向右移动一位，原来的数就扩大10倍；小数点向右移动两位，原来的数就扩大100倍；小数点向右移动三位，原来的数就扩大1000倍……

　　2、小数点向左移动一位，原来的数就缩小10倍；小数点向左移动两位，原来的数就缩小100倍；小数点向左移动三位，原来的数就缩小1000倍……

　　3、小数点向左移或者向右移位数不够时，要用“0″补足位。

　　（四）分数的基本性质

　　分数的基本性质：分数的分子和分母都乘以或者除以相同的数（零除外），分数的大小不变。

　　（五）分数与除法的关系

　　1、被除数÷除数= 被除数/除数

　　2、因为零不能作除数，所以分数的分母不能为零。

　　3、被除数 相当于分子，除数相当于分母。

六年级数学公式全部人教版

一、根据图形的形状求面积：

1. 正方形面积公式：正方形的面积=边长的平方

2. 长方形面积公式：长方形面积=长×宽

3. 圆形面积公式：圆形面积=π×半径的平方

4. 三角形面积公式：三角形面积=（底×高）÷2

5. 梯形面积公式：梯形面积=（上底+下底）×高÷2

二、数列与等比数列：

1. 等差数列求和公式：Sn=（a1+an）×n÷2

2. 等比数列求和公式：Sn=a1×（1-q^n）÷（1-q）

3. 等比数列的前n项和公式：Sn=a1×（1-q^n）÷（1-q）

4. 等比数列中第n项公式：an=a1×q^（n-1）

三、指数函数：

1. 指数函数定义公式：y=a·b^x（a>0，b>0，b≠1）

2. 指数函数方程解法：设y=a·b^x，解得x=log_ba·y

3. 指数函数导数公式：y‘=（ln b）·b^x·a

四、几何概念类：

1. 矩形的对角线公式：对角线的长度=根号（边长的平方之和）

2. 全等三角形的充分必要条件：两边之和大于第三边；所有相邻的三角形的两角之和等于180°；所有的边长相等

3. 直角三角形充要条件：两边之和大于第三边；有一个内角等于90°；腰长和底长之间若满足勾股定理则成立

4. 锐角三角形充要条件：两边之和大于第三边；所有内角都小于90°；腰长和底长之间若满足勾股定理则成立

六年级数学路程问题应用题及答案

1. （3分）一辆货车从甲地开往乙地，平均每小时行55千米．当这辆货车行了全程的20%时，如果再行79.2千米，那么已行的路程与全程的比正好是3：5．这辆货车从甲地到乙地要行多少时间？

【答案】3.6小时．

【解析】当这辆货车行了全程的20%时，如果再行79.2千米，那么已行的路程与全程的比正好是3：5，也就是已行的路程是全程的，79.2千米占全程的﹣20%，用除法得出甲乙两地的路程，再除以货车的速度即可得这辆货车从甲地到乙地要行的时间．

解：79.2÷（﹣20%）

=79.2÷40%

=198（千米），

198÷55=3.6（小时），

答：这辆货车从甲地到乙地要行3.6小时．

点评：本题考查了简单的行程问题﹣比的应用．得出79.2千米占全程的﹣20%．

2. （5分）快、慢两车同时从相距480千米的两地相向而行，3小时后还相距全程的﹣，照这样的速度，两车还要经过几小时才能相遇？

【答案】6小时

【解析】3小时后还相距全程的，即两车三小时共行了全程的1﹣，根据分数除法的意义，两车共行全程即相遇需要3÷（1﹣）小时，所以照这样的速度，两车还要经过3÷（1﹣）﹣3小时才能相遇．

解：3÷（1﹣）﹣3

=3﹣3

=9﹣3

=6（小时）

答：两车还需要6小时相遇．

点评：完成本题根据分数除法的意义求出共需多少时间较简便，不需要计算具体速度．

3. 有一座时钟现在显示10时整．那么，经过多少分钟，分针与时针第一次重合；再经过多少分钟，分针与时针第二次重合?

【答案】经过分钟，时针与分针第一次重合；经过时针与分针第二次重合。

【解析】在lO点时，时针所在位置为刻度10，分针所在位置为刻度12；当两针重合时，分针必须追上50个小刻度，设分针速度为“l”，有时针速度为“”，于是需要时间：。所以，再过分钟，时针与分针将第一次重合．第二次重合时显然为12点整，所以再经过分钟，时针与分针第二次重合。标准的时钟，每隔分钟，时针与分针重合一次。 我们来熟悉一下常见钟表(机械)的构成：一般时钟的表盘大刻度有12个，即为小时数；小刻度有60个，即为分钟数．所以时针一圈需要12小时，分针一圈需要60分钟(1小时)，时针的速度为分针速度的．如果设分针的速度为单位“l”，那么时针的速度为“”。

4. 一辆客车与一辆货车同时从甲、乙两个城市相对开出，客车每小时行46千米，货车每小时行48千米。3.5小时两车相遇。甲、乙两个城市的路程是多少千米？

【答案】329千米

【解析】本题是简单的相遇问题，根据相遇路程等于速度和乘以相遇时间得到甲乙两地路程为：（46+48）×3.5=94×3.5=329（千米）．

5. 大头儿子的家距离学校3000米，小头爸爸从家去学校接大头儿子放学，大头儿子从学校回家，他们同时出发，小头爸爸每分钟比大头儿子多走24米，50分钟后两人相遇，那么大头儿子的速度是每分钟走多少米？

【答案】18米

【解析】大头儿子和小头爸爸的速度和：(米/分钟)，小头爸爸的速度：(米/分钟)，大头儿子的速度：(米/分钟)．

6. 甲、乙两列火车从相距千米的两地相向而行，甲车每小时行千米，乙车每小时行千米，乙车先出发小时后，甲车才出发．甲车行几小时后与乙车相遇？

【答案】8小时

【解析】甲、乙两车出发时间有先有后，乙车先出发小时，这段时间甲车没有行驶，那么乙车这小时所行的路程不是甲、乙两车同时相对而行的路程，所以要先求出甲、乙两车同时相对而行的路程，再除以速度和，才是甲、乙两车同时相对而行的时间．乙车先行驶路程：(千米)，甲、乙两车同时相对而行路程：(千米)，甲、乙两车速度和：(千米／时)， 甲车行的时间：(小时)．

7. 甲、乙两辆汽车分别从、两地出发相向而行，甲车先行3小时后乙车从地出发，乙车出发小时后两车还相距千米．甲车每小时行千米，乙车每小时行千米．求、两地间相距多少千米？

【答案】649千米

【解析】题目中写的“还”相距千米指的就是最简单的情况。画线段图如下：

由图中可以看出，甲行驶了(小时)，行驶距离为：(千米)；乙行驶了小时，行驶距离为：(千米)，此时两车还相距千米，所以、两地间相距： (千米)

也可以这样做：两车小时一共行驶：(千米)，、两地间相距： (千米)，所以，、两地间相距千米．

8. 两地相距3300米，甲、乙二人同时从两地相对而行，甲每分钟行82米，乙每分钟行83米，已经行了15分钟，还要行多少分钟两人可以相遇？

【答案】5分钟

【解析】根据题意列综合算式得到：（分钟），所以两个人还需要5分钟相遇。

9. 两列火车从相距千米的两城相向而行，甲列车每小时行千米，乙列车每小时行千米，小时后，甲、乙两车还相距多少千米？

【答案】70千米

【解析】两车的相距路程减去小时两车共行的路程，就得到了两车还相距的路程：（千米）．

10. 下午放学时，弟弟以每分钟40米的速度步行回家.5分钟后，哥哥以每分钟60米的速度也从学校步行回家，哥哥出发后，经过几分钟可以追上弟弟？（假定从学校到家有足够远，即哥哥追上弟弟时，仍没有回到家）.

【答案】10分钟

【解析】若经过5分钟，弟弟已到了A地，此时弟弟已走了40×5=200（米）；哥哥每分钟比弟弟多走20米，几分钟可以追上这200米呢？40×5÷（60-40）=200÷20=10（分钟），哥哥10分钟可以追上弟弟.

11. 哥哥和弟弟在同一所学校读书．哥哥每分钟走65米，弟弟每分钟走40米，有一天弟弟先走5分钟后，哥哥才从家出发，当弟弟到达学校时哥哥正好追上弟弟也到达学校，问他们家离学校有多远?

【答案】520米

【解析】哥哥出发的时候弟弟走了：（米），哥哥追弟弟的追及时间为：（分钟），所以家离学校的距离为：（米）.

12. 甲、乙两辆汽车同时从地出发去地，甲车每小时行千米，乙车每小时行千米．途中甲车出故障停车修理了小时，结果甲车比乙车迟到小时到达地．、两地间的路程是多少？

【答案】400千米

【解析】由于甲车在途中停车小时，比乙车迟到小时，说明行这段路程甲车比乙车少用小时．可理解成甲车在途中停车小时，两车同时到达，也就是乙车比甲车先行小时，两车同时到达地，所以，也可以用追及问题的数量关系来解答．即：行这段路程甲车比乙车少用的时间是：(小时)，乙车小时行的路程是：(千米)，甲车每小时比乙车多行的路程是：(千米)，甲车所需的时间是：(小时)，、两地间的路程是：(千米)．

13. 军事演习中，“我”海军英雄舰追及“敌”军舰，追到A岛时，“敌”舰已在10分钟前逃离，“敌”舰每分钟行驶1000米，“我”海军英雄舰每分钟行驶1470米，在距离“敌”舰600米处可开炮射击，问“我”海军英雄舰从A岛出发经过多少分钟可射击敌舰？

【答案】20分钟

【解析】“我”舰追到A岛时，“敌”舰已逃离10分钟了，因此，在A岛时，“我”舰与“敌”舰的距离为10000米（=1000×10）.又因为“我”舰在距离“敌”舰600米处即可开炮射击，即“我”舰只要追上“敌”舰9400（=10000米-600米）即可开炮射击.所以，在这个问题中，不妨把9400当作路程差，根据公式求得追及时间.（1000×10-600）÷（1470-1000）=（10000-600）÷470=9400÷470=20（分钟），经过20分钟可开炮射击“敌”舰.

14. 甲车每小时行40千米，乙车每小时行60千米。两车分别从A，B两地同时出发，相向而行，相遇后3时，甲车到达B地。求A，B两地的距离。

【答案】200千米

【解析】相遇后甲行驶了40×3=120千米，即相遇前乙行驶了120千米，说明甲乙二人的相遇时间是120÷60=2小时，则两地相距（40+60）×2=200千米．

15. 甲、乙二人分别从A、B两地同时出发，如果两人同向而行，甲26分钟赶上乙；如果两人相向而行，6分钟可相遇，又已知乙每分钟行50米，求A、B两地的距离.

【答案】780米

【解析】先画图如下：

若设甲、乙二人相遇地点为C，甲追及乙的地点为D，则由题意可知甲从A到C用6分钟.而从A到D则用26分钟，因此，甲走C到D之间的路程时，所用时间应为：（26-6）=20（分）。同时，由上图可知，C、D间的路程等于BC加BD.即等于乙在6分钟内所走的路程与在26分钟内所走的路程之和，为50×（26＋6）=1600（米）.所以，甲的速度为1600÷20＝80（米/分），由此可求出A、B间的距离。50×（26+6）÷（26-6）=50×32÷20＝80（米/分），（80+50）×6＝130×6=780（米）

16. 如图， 、是一条道路的两端点，亮亮在点，明明在点，两人同时出发，相向而行．他们在离点米的点第一次相遇．亮亮到达点后返回点，明明到达点后返回点，两人在离点米的点第二次相遇．整个过程中，两人各自的速度都保持不变．求 、间的距离．要求写出关键的推理过程．

【答案】220米。见解析

【解析】第一次相遇，两人共走了一个全程，其中亮亮走了米，从开始到第二次相遇，两人共走了三个全程，则亮亮走了(米)．亮亮共走的路程为一个全程多米，所以道路长（米）．

17. 上午8点8分，小明骑自行车从家里出发，8分钟后，爸爸骑摩托车去追他，在离家4千米的地方追上了他．然后爸爸立即回家，到家后又立刻回头去追小明，再追上小明的时候，离家恰好是8千米，这时是几点几分？

【答案】8点32分

【解析】画一张简单的示意图：

图上可以看出，从爸爸第一次追上到第二次追上，小明骑了(千米)．而爸爸骑的距离是 (千米)．

这就可以知道，爸爸骑摩托车的速度是小明骑自行车速度的倍．按照这个倍数计算，小明骑8千米，爸爸可以骑行(千米)．但事实上，爸爸少用了8分钟，骑行了(千米)，少骑行(千米)．摩托车的速度是(千米/分)，爸爸骑行16千米需要16分钟．(分钟)．所以这时是8点32分．

18. 两个码头相距352千米，一船顺流而下，行完全程需要11小时.逆流而上，行完全程需要16小时，求这条河水流速度。

【答案】5千米/小时

【解析】（352÷11-352÷16）÷2=5（千米/小时）．

19. 光明号渔船顺水而下行200千米要10小时，逆水而上行120千米也要10小时．那么，在静水中航行320千米需要多少小时？

【答案】20小时

【解析】顺水速度：（千米/时），逆水速度：（千米/时），静水速度：（千米/时），该船在静水中航行320千米需要（小时）．

20. 一只船在河里航行，顺流而下每小时行千米．已知这只船下行小时恰好与上行小时所行的路程相等．求船速和水速．

【答案】船速15千米/小时，水速3千米/小时

【解析】这只船的逆水速度为：(千米/时)；船速为：(千米/时)；水流速度为：(千米/时)

21. A、 B 两码头间河流长为 220 千米，甲、乙两船分别从 A、 B 码头同时起航．如果相向而行 5 小时相遇，如果同向而行 55小时甲船追上乙船．求两船在静水中的速度．

【答案】甲船24千米/小时，乙船20千米/小時

【解析】相向而行时的速度和等于两船在静水中的速度之和，同向而行时的速度差等于两船在静水中的速度之差，所以，两船在静水中的速度之和为： 220÷ 5= 44(千米/时)，两船在静水中的速度之差为：220÷ 55 =4(千米/时)，甲船在静水中的速度为： (44 ＋4)÷ 2 =24(千米/时)，乙船在静水中的速度为： (44－ 4) ÷2 =20(千米/时)．

22. 某人畅游长江，逆流而上，在处丢失一只水壶，他向前又游了分钟后，才发现丢失了水壶，立即返回追寻，在离处千米的地方追到，则他返回寻水壶用了多少分钟？

【答案】20分钟

【解析】此人丢失水壶后继续逆流而上分钟，水壶则顺流而下，两者速度和此人的逆水速度水速此人的静水速度水速水速此人的静水速度，此人与水壶的距离两者速度和时间．此人发现水壶丢失后返回，与水壶一同顺流而下．两者速度差等于此人的静水速度，故等于丢失水壶后至返回追寻前的两者速度和，而追及距离即此人发现水壶丢失时与水壶的距离，所以追及时间等于丢失水壶后至发现丢失并返回追寻的这一段时间，即分钟．

23. 一条河上有甲、乙两个码头，甲在乙的上游 50 千米处。客船和货船分别从甲、乙两码头出发向上游行驶，两船的静水速度相同且始终保持不变。客船出发时有一物品从船上落入水中，10 分钟后此物距客船 5 千米。客船在行驶 20 千米后折向下游追赶此物，追上时恰好和货船相遇。求水流的速度。

【答案】6千米/小时

【解析】5÷1/6=30(千米/小时)，所以两处的静水速度均为每小时 30 千米。 50÷30=5/3(小时)，所以货船与物品相遇需要5/3小时，即两船经过5/3小时候相遇。 由于两船静水速度相同，所以客船行驶 20 千米后两船仍相距 50 千米。 50÷(30+30)=5/6(小时)，所以客船调头后经过5/6小时两船相遇。 30-20÷(5/3-5/6)=6(千米/小时)，所以水流的速度是每小时 6 千米。

24. 甲船在静水中的船速是10千米／时，乙船在静水中的船速是千米／时．两船同时从港出发逆流而上，水流速度是千米／时，乙船到港后立即返回．从出发到两船相遇用了小时，问：，两港相距多少千米？

【答案】24千米

【解析】乙船逆水时候的速度(千米／时)，甲船逆水时候的速度(千米／时)，两船逆水速度比为：，所以乙船到港时甲船行了．乙船顺水速度与甲船逆水速度比为：，乙船返回到两船相遇，乙船行了，所以甲船小时共行了，，两港相距(千米)．

25. 甲、乙两班同学到42千米外的少年宫参加活动，但只有一辆汽车，且一次只能坐一个班的同学，已知学生步行速度相同为千米／小时，汽车载人速度是千米／小时，空车速度是千米/小时．如果要使两班同学同时到达，且到达时间最短，那么这个最短时间是多少？

【答案】2小时

【解析】

行车路线如图所示，设甲、乙两班步行的路程为1，车开出后返回接乙班．

由车与乙相遇的过程可知：，解得，

因此，车开出千米后，放下甲班回去接乙班，甲班需步行千米，共用小时．

26. 甲乙两人同时从学校出发去距离33千米外的公园，甲步行的速度是每小时4千米，乙步行的速度是每小时3千米。他们有一辆自行车，它的速度是每小时5千米，这辆车只能载一个人，所以先让其中一人先骑车到中途，然后把车放下之后继续前进，等另一个人赶到放车的位置后再骑车赶去，这样使两人同时到达公园。那么放车的位置距出发点多少千米？

【答案】9千米或24千米

【解析】根据两人到达公园所花时间相等这一等量关系可列出方程，设放车的位置距出发点x千米，如果甲先骑车,方程为：，如果乙先骑车,方程为：，两条方程分别解得x=9和x=24，所以有9千米和24千米两种答案.

27. A、B两地相距30千米，甲乙丙三人同时从A到B，而且要求同时到达。现在有两辆自行车，但不许带人，但可以将自行车放在中途某处，后来的人可以接着骑。已知骑自行车的平均速度为每小时20千米，甲步行的速度是每小时5千米，乙和丙每小时4千米，那么三人需要多少小时可以同时到达？

【答案】3.3小时

【解析】因为乙丙步行速度相等，所以他们两人步行路程和骑车路程应该是相等的。对于甲因为他步行速度快一些，所以骑车路程少一点，步行路程多一些。现在考虑甲和乙丙步行路程的距离。甲多步行1千米要用小时，乙多骑车1千米用小时，甲多用小时。甲步行1千米比乙少用小时，所以甲比乙多步行的路程是乙步行路程的：.

这样设乙丙步行路程为3份，甲步行4份。如下图安排：

这样甲骑车行骑车的，步行. 所以时间为：小时。

28. 在双轨铁道上，速度为千米/小时的货车时到达铁桥，时分秒完全通过铁桥，后来一列速度为千米/小时的列车，时分到达铁桥，时分秒完全通过铁桥，时分秒列车完全超过在前面行使的货车．求货车、列车和铁桥的长度各是多少米？

【答案】480 280 780

【解析】先统一单位：千米/小时米/秒，千米/小时米/秒，

分秒秒，分秒分分秒秒．

货车的过桥路程等于货车与铁桥的长度之和，为：(米)；

列车的过桥路程等于列车与铁桥的长度之和，为：(米)．

考虑列车与货车的追及问题，货车时到达铁桥，列车时分到达铁桥，在列车到达铁桥时，货车已向前行进了12分钟(720秒)，从这一刻开始列车开始追赶货车，经过2216秒的时间完全超过货车，这一过程中追及的路程为货车12分钟走的路程加上列车的车长，所以列车的长度为(米)，那么铁桥的长度为(米)，货车的长度为(米)．

29. 如图,学校操场的400米跑道中套着300米小跑道,大跑道与小跑道有200米路程相重．甲以每秒6米的速度沿大跑道逆时针方向跑,乙以每秒4米的速度沿小跑道顺时针方向跑,两人同时从两跑道的交点处出发,当他们第二次在跑道上相遇时,甲共跑了多少米?

【答案】660

【解析】根据题意可知，甲、乙只可能在右侧的半跑道上相遇．

易知小跑道上左侧的路程为100米,右侧的路程为200米,大跑道上的左、右两侧的路程均是200米．

我们将甲、乙的行程状况分析清楚．

当甲第一次到达点时,乙还没有到达点,所以第一次相遇一定在逆时针的某处．

而当乙第一次到达点时，所需时间为秒,此时甲跑了米,在离点米处．

乙跑出小跑道到达点需要秒,则甲又跑了米,在点左边米处．

所以当甲再次到达处时,乙还未到处,那么甲必定能在点右边某处与乙第二次相遇．

从乙再次到达处开始计算,还需秒,甲、乙第二次相遇,此时甲共跑了秒．

所以，从开始到甲、乙第二次相遇甲共跑了米．

30. 甲、乙两车分别同时从A、B两地相对开出，第一次在离A地95千米处相遇．相遇后继续前进到达目的地后又立刻返回，第二次在离B地25千米处相遇．求A、B两地间的距离是多少千米？

【答案】260

【解析】画线段示意图(实线表示甲车行进的路线，虚线表示乙车行进的路线)：

可以发现第一次相遇意味着两车行了一个A、B两地间距离，第二次相遇意味着两车共行了三个A、B两地间的距离．当甲、乙两车共行了一个A、B两地间的距离时，甲车行了95千米，当它们共行三个A、B两地间的距离时，甲车就行了3个95千米，即95×3=285（千米），而这285千米比一个A、B两地间的距离多25千米，可得：95×3-25=285-25=260(千米)．

六年级数学相遇问题解题技巧

1、甲车的速度与乙车的速度比是3:4，两车从A、B两地同时相向而行，在距离中点5千米处相遇，问A、B两地之间的路程是多少？

2、一个人沿直街走，每2分钟迎面开来一辆公共汽车，每8分钟身后开来一辆公共汽车，公共汽车的速度相同，则公共汽车站每隔多少分钟发一辆公共汽车？

刘明骑自行车从家到学校，每小时行18千米，回来时是逆风，每小时行12千米，他往返这段路平均每小时行多少千米？

3、一架名航班机在两城之间往返一次3.8小时，飞去的速度为每小时500千米，飞回的速度为每小时450千米，两城相距多少千米？（请利用所学的知识，选择至少三种方法解答）

4、从A城到B城，甲车要10小时，乙车要8小时，甲车速度比乙车（ ）

A、快25％ B、慢20％ C、慢80％

5、一列火车从北京开往上海，3小时行了全程的，这时距中点还有40千米，这列火车平均每小时行多少千米？

6、甲、乙两车分别从A、B两地同时相向而行，甲每小时行80千米,乙每小时行全程的10％,当乙行到全程的时，甲车再行全程的,可到达B地，求A、B两地相距多少千米？

7、甲、乙、丙三个小运动员参加100米赛跑，当甲到达终点时，乙离终点还有5米，当乙到达终点时，丙离终点还有5米，那么，当甲到达终点时，丙离终点还有（ ）米

A、10米 B、9.75米 C、9.25米 D、10.25米

8、一列快车从甲地开往乙地，需要6小时，慢车从乙地开往甲地需要9小时。

两车分别从两地同时开出，相向（相对）而行，在离中点

18千米处相遇，甲、乙两地相距多少千米？

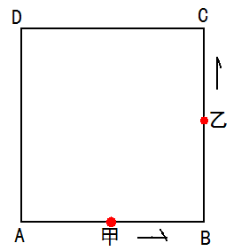
9、甲、乙两人分别从周长为1600米的正方形水池ABCD相对

的两个定点A、C，同时从出发地绕池边沿的方向行走，甲每分

走50米，乙每分走34米，则甲第一次追上乙在（ ）边上。

10、客车和货车分别从甲、乙两站同时相向而开，5小时后相遇，相遇后，两车仍按原速度前进，当它们相距196千米时，客车行了全程的，货车行了全程的80％。求货车行完全程需要多少小时？

11、甲、乙二人分别从A、B两地同时出发，相向而行，乙的速度是甲速度的，二人相遇后继续行进，甲到达B地和乙到达A地后都立即沿原路返回，已知二人第二次相遇的地点距第一次相遇的地点60千米，则A、B两地相距多少千米？

12、客车和货车同时从A、B两地相对开出。客车每小时行驶50千米，货车的速度是客车的80％，相遇后客车继续行3.2小时到达B地。A、B两地相距多少千米？

13、甲、乙两地相距450千米，两列火车同时从两地相对开出，4.5小时相遇，快车与慢车的速度比是3:2,求慢车的速度。

14、成都出租车起步价7元（路程在3千米以内），超过3千米的路程，每千米1.6元，小华坐出租车从家去体育馆，一共付车费21.4元，小华家到体育馆的路程大约有多少千米？

15、一辆大巴从广州开往韶关，行了一段路程后，离韶关还有210千米，接着又行了全程的20％，这时已行路程与未行路程的比是3:2.广州、韶光两地相距多少千米？

16、甲乙两地相距420千米，甲车从甲地出发开往乙地，每小时行72千米，25分钟后乙车从乙地出发开往甲地，每小时行28千米，两车相遇时甲车行了多少小时？

17、一条路全长60千米，分成上坡、平路、下坡三段，各段路程长的比依次是1:2:3，某人走各段路程所用时间之比依次是4:5:6，已知他上坡的速度是每小时3千米，问此人走完全程用了多少时间？

18、在一副1:20000000的地图上量的甲乙两地相距4厘米，一辆车以80km/h的速度从甲地到乙地，问几小时能行完全程？

19、明明和东东进行100米的赛跑，当明明到达终点时，东东距终点还有10米，如果明明从起点后退10米，两人同时起跑，谁先到达终点？（通过计算，说明理由）

20、兄弟两人早晨7时同时从家里出发去上学，兄每分钟走100米，弟每分钟走60米，兄到了学校后休息了5分钟才发现英语书没带，立即回家，途中7时25分与弟相遇，学校离家有多远？

21、一铁路巡道工正在隧道中工作，突然听到一列火车向隧道驶来，他立即看隧道内的路标，知道他与火车驶来方向的那端隧道口间的距离为隧道全长的。凭他的经验，用最快的速度无论向哪一头跑，当火车到达他跟前时，都刚好离开隧道，如果火车速度为每小时70千米，请问巡道工奔跑的速度是每小时多少千米？

22、环绕小山一周的公路长1920米，甲、乙两人沿公路竞走，两人同时同地出发，反向行走，甲比乙走得快，12分钟后两人相遇，如果两人每分钟都多走16米，则相遇的地点与前次相差20米。

（1）求甲乙两人原来的行走速度

（2）如果甲、乙两人各以原速度同时同地出发，同向行走，则甲在何处第二次追上乙？

23、甲从A地出发前往B地，乙、丙两人从B地出发前往A地，甲行了60千米后，乙和丙才同时从B地出发，结果甲和乙相遇在C地，甲和丙相遇在D地。已知甲的速度是丙的4倍，是乙的2倍，C、D两地之间的距离是30千米。那么A、B两地之间的距离是多少千米？

24、甲、乙、丙三车的速度分别为100千米/小时、80千米/小时、70千米/小时，甲、乙同在A地，丙在B地，三车同时出发，甲、乙、丙相向而行，丙遇到甲12分钟后又遇到乙，求A、B两地之间的距离。

25、一辆汽车从甲地开往乙地，已经行了2小时，这时距乙地还有30千米才到达，已知第一小时行的路程是第二小时与剩下路程和的，第二小时行的恰好是第一小时行的与剩下路程之和。甲乙两地全程多少千米？

26、上午八时，张、王两同学分别从A、B两地同时骑摩托车出发，相向而行，已知张每小时比王多行2千米，到上午十时，两人仍相距36千米的路程，相遇后，两人停车闲谈了15分钟，再同时按各自的方向和原来的速度继续前进，到中午十二时十五分，两人又相距36千米的路程。(1)张、王二人的速度分别为多少？(2)A、B两地间的路程有多少千米？(3)两人第一次相遇在何时？

27、一辆汽车从甲地开往乙地，每分钟行750米，预计50分钟到达。但汽车行驶到路程时，出了故障，用5分钟修理完毕，如果仍需在预定时间内到达乙地，汽车行驶余下的路程时，每分钟必须比原来快多少米？

28、有三个好朋友8月1日去图书馆借书，以后甲每隔2天去一次，乙每隔3天去一次，丙每隔4天去一次，那么他们下一次同时去图书馆的日期是多久？

29、甲、乙两人骑车分别从A、B两地同时出发相向而行。甲以每小时40千米的速度行驶，乙的速度是甲的一半，出发2小时后两人相遇并继续前进，在他们相遇5分钟后，甲在途中与迎面来的丙相遇，丙在与甲相遇后继续前进，在C地赶上乙，如果开始时，甲的速度是24千米/时，而乙的速度比原速每小时快2千米，那么甲、乙就会在C地相遇，求丙的骑车速度？

30、A、B两地相距176千米，其间一处因山体滑坡导致连接这两地的公路受阻，甲乙两个工程队接到指令，要求早上8时，分别从A、B两地同时出发赶往滑坡点疏通公路，10时，甲队赶到立即开始作业，半小时后乙队赶到，并迅速投入“战斗”，与甲队共同作业，此时与甲队完成。（1）若滑坡受损公路长1千米，甲队行进的速度是乙队的1.5倍多5千米，求甲、乙两队赶路的速度。（2）假设下午四时两队就完成任务，若只有乙队疏通公路，那要多少小时才能完成任务？

31、春运期间，笑笑准备乘坐K452次列车从成都回乌鲁木齐的家中过年，她从网上订到一张平时票价550元的硬卧下铺，为此，她要支付的火车票款时多少钱？（春运期间，硬座票价上浮15%，其他票价上浮20%）

32、甲乙两车分别从A、B两地同时相对开出，3小时后在距中点36千米处相遇，已知甲、乙两车速度比是3:2，A、B两地相距多少千米？（提示：记得画图帮助自己理解题意哟）

33、乘坐国内航班每位旅客的免费行李额：经济舱旅客为20千克，公务舱旅客为30千克，头等舱旅客为40千克，携带行李超过规定重量的部分，每千克按照飞机票价的1.5%购买行李票，笑话的爸爸从成都乘飞机飞到北京，购买经济舱机票，飞机票打八折后是1160元，他携带了30千克行李，应付行李费多少元？

34、一辆客车从A地到B地，上午出发行驶了一段路后中午停车休息1小时，已行驶路程是未行驶路程的，下午行的路程比上午行的还多56千米，这时已行的路程与还未行的路程比是11:9，A、B两地相距多少千米？

35、两辆汽车同时从某地出发，运送一批货物到距离165千米的工地，甲车比乙车早到48分钟，当甲车到达时，乙车还距工地24千米，甲车行完全程用了多少小时？

36、两辆汽车同时从A、B两站相向而开出，第一次在离A站60千米的地方相遇，之后，两车继续以原来的速度前进，各自到达对方车站后都立即返回，又在距中点右侧30千米处相遇。两站相距多少千米?

37、A、B两地相距960米，甲、乙两人分别从A、B两地同时出发，若相向而行，6分钟相遇，若同向行走，80分钟甲可以追上乙。甲从A地走到B地要多少分钟？

38、在一个600米长的环形跑道上，兄弟两人如果同时从同一起点按顺时针方向跑步，每隔12分钟相遇一次，如果两人同时从同一起点反方向跑步，每隔4分钟相遇一次，兄弟两人跑一圈各要几分钟？

39、客车和货车同时从A、B两地相对开出，客车每小时行驶50千米，货车的速度是客车的80%，相遇后客车继续行3.2小时到达B地，A、B两地相距多少千米？

40、从甲地到乙地的路程分为上坡、平路、下坡三段，各段路程之比是1:2:3，某人走这三段路所用时间之比是4:5:6，已知他上坡时的速度为每小时2.5千米，路程全长为20千米，此人从甲地走到乙地许多长时间？

41、甲、乙两人分别从A、B两地出发，相向而行，出发时他们的速度比是3:2,他们第一次相遇后，甲的速度提高了20%，乙的速度提高了30%，这样，当甲到达B地时，乙离A地还有14千米，那么A、B两地之间的距离是多少千米？

42、一辆汽车从甲地开往乙地，如果把车速度提高20%，可以比原定时间提前1小时到达，如果按原速行驶120千米后，再将速度提高25%，则可提前40分钟到达，那么甲、乙两地相距多少千米？

六年级数学必考难题带答案

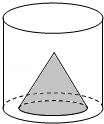
1．如图，一个底面直径是10厘米的圆柱形容器装满水．先将一个底面直径是8厘米的圆锥形铁块放入容器中，铁块全部浸入水中，再将铁块取出，这时水面的高度下降了3.2厘米．圆锥形铁块的高　　　　厘米．

2．（15分）一个棱长为6的正方体被切割成若干个棱长为整数的小正方体，若这些小正方体的表面积之和是切割前的大正方体的表面积的倍，求切割成小正方体中，棱长为1的小正方体的个数？

3．快车和慢车同时从甲、乙两地相对开出，快车每小时行33千米，相遇行了全程的，已知慢车行完全程需要8小时，则甲、乙两地相距　　千米．

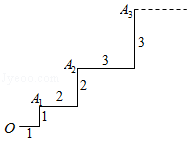
4．如图，一只玩具蚂蚁从O点出发爬行，设定第n次时，它先向右爬行n个单位，再向上爬行n个单位，达到点A_n，然后从点A_n出发继续爬行，若点O记为（0，0），点A₁记为（1，1），点A₂记为（3，3），点A₃记为（6，6），…，则点A₁₀₀记为　　　　．

5．若将算式9×8×7×6×5×4×3×2×1中的一些“×”改成“÷”使得最后的计算结果还是自然数，记为N，则N最小是　　　．

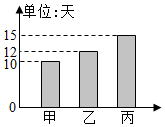
6．如图是甲乙丙三人单独完成某项工程所需天数的统计图，根据图中信息计算，若甲先做2天，接着乙丙两人合作了4天，最后余下的工程由丙1人完成，则完成这项工程共用　　　　天．

7．某日是台风天气，雨一直均匀地下着，在雨地里放一个如图1所示的长方体容器，此容器装满雨水需要1小时．

请问：雨水要下满如图2所示的三个不同的容器，各需要多长时间？

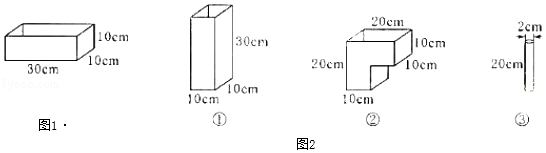
8．一根绳子，第一次剪去全长的，第二次剪去余下部分的30%．若两次剪去的部分比余下的部分多0.4米，则这根绳子原来长　　 　米．

9．根据图中的信息可知，这本故事书有　　页页．

10．已知三个分数的和是，并且它们的分母相同，分子的比是2：3：4．那么，这三个分数中最大的是　　．

11．从12点整开始，至少经过　　分钟，时针和分针都与12点整时所在位置的夹角相等．（如图中的∠1＝∠2）．

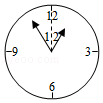
12．已知自然数N的个位数字是0，且有8个约数，则N最小是　　．

13．如图，一个直径为1厘米的圆绕边长为2厘米的正方形滚动一周后回到原来的位置．在这个过程中，圆面覆盖过的区域（阴影部分）的面积是　　　　平方厘米．（π取3）

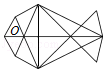
14．如图所示的“鱼”形图案中共有　　个三角形．

15．已知A是B的，B是C的，若A+C＝55，则A＝　　　　．

16．从1，2，3，…，2016中任意取出n个数，若取出的数中至少有两个数互质，则n最小是　　　　．

17．能被5和6整除，并且数字中至少有一个6的三位数有　　　　个．

18．小红买1支钢笔和3个笔记本共用了36.45元，其中每个笔记本售价的与每支钢笔的售价相等，则1支钢笔的售价是　　　　元．

19．a，b，c是三个互不相等的自然数，且a+b+c＝48，那么a，b，c的乘积最大是　　　　．

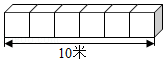
20．如图，将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，这根长方体木块原来的体积是　　　　立方分米．

21．2015减去它的，再减去余下的，再减去余下的，…，最后一次减去余下的，最后得到的数是　　　　．

22．已知两位数与的比是5：6，则＝　　　　．

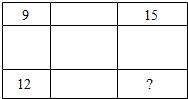
23．如图，将1个大长方形分成了9个小长方形，其中位于角上的3个小长方形的面积分别为9，15和12，由第4个角上的小长方形的面积等于　　　　．

24．某项工程，开始由6人用35天完成了全部工程的，此后，增加了6人一起来完成这项工程．则完成这项工程共用　　　　天．

25．在救灾捐款中，某公司有的人各捐200元，有的人各捐100元，其余人各捐50元．该公司人均捐款　　　　元．

26．1²⁰¹³+2²⁰¹³+3²⁰¹³+4²⁰¹³+5²⁰¹³除以5，余数是　 　　　．（a²⁰¹³表示2013个a相乘）

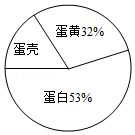
27．如图是根据鸡蛋的三个组成部分的质量绘制的扇形统计图，由图可知，蛋壳重量占鸡蛋重量的　 　　%，一枚重60克的鸡蛋中，最接近32克的组成部分是　 　　．

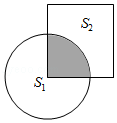
28．如图，边长为12cm的正方形与直径为16cm的圆部分重叠（圆心是正方形的一个顶点），用S₁，S₂分别表示两块空白部分的面积，则S₁﹣S₂＝　 　　cm²（圆周率π取3）．

29．定义新运算“*”：a*b＝

例如3.5*2＝3.5，1*1.2＝1.2，7*7＝1，则 ＝　 　　．

30．张阿姨和李阿姨每月的工资相同，张阿姨每月把工资的30%存入银行，其余的钱用于日常开支，李阿姨每月的日常开支比张阿姨多10%，余下的钱也存入银行，这样过了一年，李阿姨发现，她12个月存入银行的总额比张阿姨少了5880元，则李阿姨的月工资是　 　　　元．

31．A，B两校的男、女生人数的比分别为8：7和30：31，两校合并后男、女生人数的比是27：26，则A，B两校合并前人数比是 　　　．

32．从12点开始，经过　 　　　分钟，时针与分针第一次成90°角；12点之后，时针与分针第二次成90°角的时刻是　 　　．

33．若一个长方体，长是宽的2倍，宽是高的2倍，所有棱长之和是56，则此长方体的体积是　 　　　．

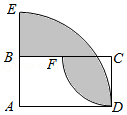
34．图中阴影部分的两段圆弧所对应的圆心分别为点A和点C，AE＝4m，点B是AE的中点，那么阴影部分的周长是　 　　　m，面积是　 　　　m²（圆周率π取3）．

35．小红整理零钱包时发现，包中有面值为1分，2分，5分的硬币共有25枚，总值为0.60元，则5分的硬币最多有　 　　　枚．

36．宏富超市购进一批食盐，第一个月售出这批盐的40%，第二个月又售出这批盐的420袋，这时已售出的和剩下食盐的数量比是3：1，则宏富超市购进的这批食盐有　 　　　袋．

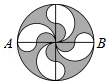
37．如图，已知AB＝40cm，图中的曲线是由半径不同的三种半圆弧平滑连接而成，那么阴影部分的面积是　　cm²．（π取3.14）

38．有两辆火车，车长分别是125米和115米，车速分别是22米/秒和18米/秒，两车相向行驶，从两车车头相遇到车尾分开需要　 　　　秒．

39．建筑公司建一条隧道，按原速度建成时，使用新设备，使修建速度提高了20%，并且每天的工作时间缩短为原来的80%，结果共用185天建完隧道，若没有新设备，按原速度建完，则需要 　天．

40．从1开始的n个连续的自然数，如果去掉其中的一个数后，余下的各个数的平均数是，那么去掉的数是　 　　　．

41．若A、B、C三种文具分别有38个，78和128个，将每种文具都平均分给学生，分完后剩下2个A，6个B，20个C，则学生最多有 　　人．

42．（15分）王老师将200块糖分给了甲乙丙三个小朋友，甲比乙的2倍还要多，乙比丙的3倍还要多，那么甲最少有　 　　　块糖，丙最多有　 　　　块糖．

43．（15分）欢欢、乐乐、洋洋参加希望之星决赛，有200位评委为他们投了票，每位评委只投一票．如果欢欢与乐乐所得票数的比是3：2，乐乐与洋洋所得票数的比是6：5，那么欢欢、乐乐、洋洋各得多少票？

44．一列快车从甲地开往乙地需要5小时，一列慢车从乙地开往甲地所需时间比快车多，两车同时从甲乙两地相对开出2小时后，慢车停止前进，快车继续行驶40千米后恰与慢车相遇，则甲乙两地相距　　千米．

45．对任意两个数x，y，定义新的运算*为： （其中m是一个确定的数）．如果，那么m＝　　，2*6＝　　．

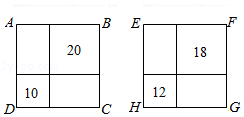
46．如图，正方形ABCD和EFGH分别被互相垂直的直线分为两个小正方形和两个矩形，小正方形的面积的值已标在图中，分别为20和10，18和12，则正方形ABCD和EFGH中，面积较大的正方形是　　．

47．某工程队修建一条铁路隧道，当完成任务的时，工程队采用新设备，使修建速度提高了20%，同时为了保养新设备，每天工作时间缩短为原来的，结果，前后共用185天完工，由以上条件可推知，如果不采用新设备，完工共需　　天．

48．王老师在黑板上写了若干个从1开始的连续自然数：1，2，3，4，…，然后擦去三个数（其中有两个质数），如果剩下的数的平均数是19，那么王老师在黑板上共写了　39　个数，擦去的两个质数的和最大是　　．

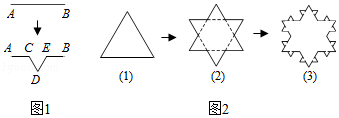
49．对于一个多边形，定义一种“生长”操作：如图1，将其一边AB变成向外凸的折线ACDEB，其中C和E是AB的三等分点，C，D，E三点可构成等边三角形，那么，一个边长是9的等边三角形，经过两次“生长”操作（如图2），得到的图形的周长是　　；经过四次“生长”操作，得到的图形的周长是　　．

50．如图，三个同心圆分别被直径AB，CD，EF，GH八等分，那么，图中阴影部分面积与非阴影部分面积之比是　 　　．

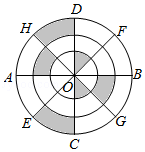
【参考答案】

一、小学数学小升初难题精选

1．解：圆锥形铁块的体积是：

3.14×（10÷2）²×3.2

＝3.14×25×3.2

＝251.2（cm³）

铁块的高是：251.2×3÷[3.14×（）²]

＝251.2×3÷50.24

＝15（cm）

答：铁块的高是15cm．

2．解：大正方体表面积：6×6×6＝216，

体积是：6×6×6＝216，

切割后小正方体表面积总和是：216×＝720，

假设棱长为5的小正方体有1个，那么剩下的小正方体的棱长只能是1，个数是：（6³﹣5³）÷1³＝91（个），这时表面积总和是：5²×6+1²×6×91＝696≠720，所以不可能有棱长为5的小正方体．

（1）同理，棱长为4的小正方体最多为1个，此时，不可能有棱长为3的小正方体，剩下的只能是切割成棱长为2的小正方体或棱长为1的小正方体，

设棱长为2的小正方体有a个，棱长为1的小正方体有b个，

则

解得：

（2）棱长为3的小正方体要少于（6÷3）×（6÷3）×（6÷3）＝8个，

设棱长为2的小正方体有a个，棱长为1的小正方体有b个，棱长为3的小正方体有c个，

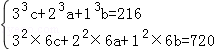
化简：

由上式可得：

b＝9c+24，a＝，

当c＝0时，b24＝，a＝24，

当c＝1时，b＝33，a＝19.5，（不合题意舍去）

当c＝2时，b＝42，a＝15，

当c＝3时，b＝51，a＝10.5，（不合题意舍去）

当c＝4时，b＝60，a＝6，

当c＝5时，b＝69，a＝28.5，（不合题意舍去）

当c＝6时，b＝78，a＝﹣3，（不合题意舍去）

当c＝7时，a＝负数，（不合题意舍去）

所以，棱长为1的小正方体的个数只能是：56或24或42或60个．

答：棱长为1的小正方体的个数只能是：56或24或42或60个．

3．解：1﹣＝

×8＝（小时）

×33＝（千米）

÷＝198（千米）

答：甲、乙两地相距198千米．

故答案为：198．

4．解：根据分析可知A₁₀₀记为（1+2+3+…+100，1+2+3+…+100）；

因为1+2+3+…+100＝（1+100）×100÷2＝5050，

所以A₁₀₀记为（5050，5050）；

故答案为：A₁₀₀记为（5050，5050）．

5．解：根据分析，先分解质因数9＝3×3，8＝2×2×2，6＝2×3，故有：

9×8×7×6×5×4×3×2×1＝（3×3）×（2×2×2）×7×（3×2）×5×（2×2）×3×2×1，

所以可变换为：9×8×7÷6×5÷4÷3×2×1＝70，此时N最小，为70，

故答案是：70．

6．解：依题意可知：

甲乙丙的工作效率分别为：，，；

甲乙工作总量为：×2+×4＝；

丙的工作天数为：（1﹣）＝3（天）；

共工作2+4+3＝9

故答案为：9

7．解：图1所示的长方体容器的容积：10×10×30＝3000（立方厘米）

接水口的面积为：10×30＝300（平方厘米）

接水口每平方厘米每小时可接水：3000÷300÷1＝10（立方厘米）

所以，图①需要：10×10×30÷（10×10×10）＝3（小时）

图②需要：（10×10×20+10×10×10）÷（10×10×20）＝1.5（小时）

图③需要：2÷2＝1（厘米）

3.14×1×1×20÷（3.14×1×10）＝2（小时）

答：容器①需要3小时，容器②需要1.5小时，容器③需要2小时．

8．解：第二次剪求的占全长的：

（1）×30%

＝

＝，

0.4÷[（1）]

＝0.4÷[]

＝

＝0.4×15

＝6（米）；

答：这根绳子原来长6米．

故答案为：6．

9．解：（10+5）÷（1﹣×2）

＝15÷

＝25（页）

答：这本故事书有25页；

故答案为：25．

10．解：

＝

＝，

答：这三个分数中最大的一个是．

故答案为：．

11．解：设所走的时间为x小时．

30x＝360﹣360x

3x+360x＝360﹣30x+360

390x＝360

x＝

小时＝55分钟．

故答案为：55．

12．解：自然数N的个位数字是0，它一定有质因数5和2，要使N最小，5的个数应最少为1个，而求其它因数最好都是2和3，并且2的个数不能超过2个，其它最好都是3；

设这个自然数N＝2¹×5¹×3^a，根据约数和定理，可得：

（a+1）×（1+1）×（1+1）＝8，

（a+1）×2×2＝8，

a＝1；

所以，N最小是：2×3×5＝30；

答：N最小是30．

故答案为：30．

13．解：2×1×4+3×1²

＝8+3

＝11（平方厘米）

答：阴影部分的面积是11平方厘米．

故答案为：11．

14．解：由一个三角形组成：14个；

由两个三角形组成：8个；

由三个三角形组成：8个；

由四个三角形组成：4个；

由六个三角形组成：1个；

总共：14+8+8+4+1＝35个．

故共有35个三角形．

故答案为：35．

15．解：A是C的×＝，

即A＝C，

A+C＝55，则：

C+C＝55

C＝55

C＝55÷

C＝40

A＝40×＝15

故答案为：15．

16．解：根据分析，1～2016数中，有奇数1008个，偶数1008个，因为偶数和偶数之间不能互质，故：

①n＜1008时，有可能取的n个数都是偶数，就不能出现至少有两个数互质的情况；

②n＝1008时，若取的数都是偶数，也不能出现至少有两个数互质的情况；

③n≥1009时，则取的n个数里至少有一个为奇数，取出的这个奇数和它相邻的偶数一定互质，

综上，n最小是1009．

故答案是：1009．

17．解：根据分析，分解质因数6＝2×3

∴这个三位数能同时被2、3、5整除，而且数字中至少含有一个6

∴这个三位数的个位数必须为偶数或0，因被5整除的数个位数必须是0或5，故个位数为0，

设此三位数为，按题意a、b中至少有一个数字为6，

①a＝6时，则6+b+0 是3的倍数，则b＝0，3，6，9，符合的三位数为：600、630、660、690

②b＝6时，则6+a+0 是3的倍数，则a＝3，6，9，符合的三位数为：360、660、960

综上所述，符合题意的三位数为：360、660、960、600、630、690

故答案为：6．

18．解：36.45÷（3+）

＝36.45

＝5.4

5.4×＝20.25（元）

答：1支钢笔的售价是 20.25元．

故答案为：20.25．

19．解：48÷3＝16，

16﹣1＝15，

16+1＝17，

所以，a，b，c的乘积最大是：15×16×17＝4080．

故答案为：4080．

20．解：依题意可知：

将一根长10米的长方体木块锯成6段，表面积比原来增加了100平方分米，变面积增加了10个面，那么每一个面的面积为100÷10＝10平方分米．

10米＝100分米．

体积为：10×100＝1000（立方分米）．

故答案为：1000

21．解：2015×（1﹣）×（1﹣）×（1﹣）×…×（1﹣）

＝2015××××…×

＝1

故答案为：1．

22．解：因为（10a+b）：（10b+a）＝5：6，

所以（10a+b）×6＝（10b+a）×5

60a+6b＝50b+5a

所以55a＝44b

则a＝b，

所以b只能为5，则a＝4．

所以＝45．

故答案为：45．

23．解：如图，

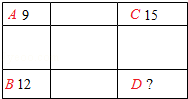
设D的面积为x，

9：12＝15：x

9x＝12×15

x＝

x＝20

答：第4个角上的小长方形的面积等于20．

故答案为：20．

24．解：总工作量看做单位“1”．剩余工作量为1﹣＝，一个人的工作效率为÷6÷35，

（1﹣）÷[÷6÷35×（6+6）]

＝÷（÷6÷35×12）

＝÷

＝35（天）

35+35＝70（天）

答：完成这项工程共用70天．

故答案为：70．

25．解：捐50元人数的分率为：1﹣＝，

（200×+100×+50×）÷1

＝（20+75+7.5）÷1

＝102.5（元）

答：该公司人均捐款102.5元．

故答案为：102.5．

26．解：多个2相乘结果个位数字有一个规律：2、4、8、6每4个2相乘一个循环，

多个3相乘结果个位数字有一个规律：3、9、7、1每4个3相乘一个循环，

2013÷4＝503…1，

所以2013个2相乘后个位数字是2，2013个3相乘后个位数字是3，2013个4相乘后个位数字是4，1的任何次方都是1，5的任何次方的个位数字都是5，1+2+3+4+5＝15

所以1²⁰¹³+2²⁰¹³+3²⁰¹³+4²⁰¹³+5²⁰¹³的个位数字是5，

所以除以5的余数是0；

故答案为：0．

27．解：（1）1﹣32%﹣53%，

＝1﹣85%，

＝15%；

答：蛋壳重量占鸡蛋重量的15%．

（2）蛋黄重量：60×32%＝19.2（克），

蛋白重量：60×53%＝31.8（克），

蛋壳重量：60×15%＝9（克），

所以最接近32克的组成部分是蛋白．

答：最接近32克的组成部分是蛋白．

故答案为：15，蛋白．

28．解：3×（16÷2）²﹣12²

＝192﹣144，

＝48（平方厘米）；

答：S₁﹣S₂＝48cm²．

故答案为：48．

29．解：根据分析可得，

，

＝，

＝2；

故答案为：2．

30．解：（1﹣30%）×（1+10%）

＝70%×110%，

＝77%；

5880÷12÷[30%﹣（1﹣77%）]

＝490÷[30%﹣23%]，

＝490÷7%，

＝7000（元）．

即李阿姨的月工资是 7000元．

故答案为：7000．

31．解：设A、B两校的男生、女生人数分别为8a、7a、30b、31b，

由题意得：

（8a+30b）：（7a+31b）＝27：26，

27×（7a+31b）＝26×（8a+30b），

189a+837b＝208a+780b，

837b﹣780b＝208a﹣189a，

57b＝19a，

所以a＝3b，

所以A、B两校合并前人数的比是：

（8a+7a）：（30b+31b），

＝15a：61b，

＝45b：61b，

＝（45b÷b）：（61b÷b）

＝45：61；

答：A，B两校合并前人数比是45：61．

故答案为：45：61．

32．解：分针每分钟走的度数是：

360÷60＝6（度），

时针每分钟走的度数是：

6×5÷60＝0.5（度），

第一成直角用的时间是：

90÷（6﹣0.5），

＝90÷5.5，

＝16（分钟），

第二次成直角用的时间是：

270÷（6﹣0.5），

＝270÷5.5，

＝49（分钟）．

这时的时刻是：

12时+49分＝12时49分．

故答案为：16，12时49分．

33．解：长方体的高是：

56÷4÷（1+2+4），

＝14÷7，

＝2，

宽是：2×2＝4，

长是：4×2＝8，

体积是：8×4×2＝64，

答：这个长方体的体积是64．

故答案为：64．

34．解：阴影部分的周长：4+3×4×2÷4+3×2×2÷4，

＝4+6+3，

＝13（米）；

阴影部分的面积：3×4²÷4+3×2²÷4﹣2×4，

＝12+3﹣8，

＝7（平方米）；

答：阴影部分的周长是13米，面积是7平方米．

故答案为：13、7．

35．解：因为0.60元＝60分，

设1分，2分，5分的硬币各有x枚、y枚和z枚，则有x+y+z＝25，x+2y+5z＝60，

把上面的两个式子相减得出y+4z＝35，要使5分的硬币最大，即Z最大，y最小，

因为35是奇数，所以y必须是奇数，

当y＝1时，z的值不是整数，

当y＝3时，z＝8，

所以z＝8；

答：5分的硬币最多有8枚；

故答案为：8．

36．解：420÷（1﹣40%﹣）

＝420÷0.35

＝1200（袋）

答：宏富超市购进的这批食盐有1200袋．

故答案为：1200．

37．解：40÷2＝20（厘米）

20÷2＝10（厘米）

3.14×20²﹣3.14×10²÷2×4

＝1256﹣628

＝628（平方厘米）

答：阴影部分的面积是628平方厘米．

故答案为：628．

38．解：（125+115）÷（22+18）

＝240÷40

＝6（秒）；

答：从两车头相遇到车尾分开需要6秒钟．

故答案为：6．

39．解：（1﹣）÷[（1+20%）×80%]

＝÷[120%×80%]，

＝，

＝；

185÷（+）

＝185÷，

＝180（天）．

答：按原速度建完，则需要180天．

故答案为：180．

40．解：设去掉的数是x，那么去掉一个数后的和是：

（1+n）n÷2﹣x＝×（n﹣1）；

显然，n﹣1是7的倍数；

n＝8、15、22、29、36时，x均为负数，不符合题意．

n＝43时，和为946，42×＝912，946﹣912＝34．

n＝50时，和为1225，49×＝1064，1225﹣1064＝161＞50，不符合题意．

答：去掉的数是34．

故答案为：34．

41．解：38﹣2＝36（个）

78﹣6＝72（个）

128﹣20＝108（个）

36、48和108的最大公约数是36，所以学生最多有36人．

故答案为：36．

42．解：甲比丙的2×3＝6倍多，总数就比丙的6+3+1＝10倍多200÷（2×3+3+1）＝20（块），

丙最多：20﹣1＝19（块）

此时甲乙至少有：200﹣19＝181（块），

181÷（2+1）＝60（块）…1（块），

乙最多60块，

甲至少：60×2+1＝121（块）．

故答案为：121，19．

43．解：根据欢欢与乐乐所得票数的比是3：2，乐乐与洋洋所得票数的比是6：5，

可以求出欢欢、乐乐、洋洋所得票数的比9：6：5，

200×＝90（票）

200×＝60（票）

200×＝50（票）

答：欢欢所得票数是90票，乐乐所得票数是60票，洋洋所得票数是50票．

44．解：慢车行完全程需要：

5×（1+），

＝5×，

＝6（小时）；

全程为：

40÷[1﹣（+）×2]，

＝40÷[1﹣]，

＝40÷，

＝40×，

＝150（千米）；

答：甲乙两地相距150千米．

故答案为：150．

45．解：（1）1*2＝＝，

即2m+8＝10，

2m＝10﹣8，

2m＝2，

m＝1，

（2）2*6，

＝，

＝，

故答案为：1，．

46．解：小正方形的面积之和为30时，两正方形的面积差最小，则大正方形的面积越大，

即EFGH的面积较大；

故答案为：EFGH．

47．解：设计划用x天完成任务，

那么原计划每天的工作效率是，提高后每天的工作效率是×（1+20%）＝×＝，

前面完成工程的所用时间是天，提高工作效率后所用的实际是（185﹣）×天，

所以，+（185﹣）××＝1，

+（185﹣）××﹣＝1﹣，

（185﹣）××＝，

（185﹣）×÷＝÷，

185﹣+＝x+，

x÷＝185÷，

x＝180，

答：工程队原计划180天完成任务．

故答案为：180．

48．解：由剩下的数的平均数是19，

即得最大的数约为20×2＝40个，

又知分母是9，所以剩下的数的个数必含因数9，则推得剩余36个数．

原写下了1到39这39个数；

剩余36个数的和：19×36＝716，

39个数的总和：（1+39）×39÷2＝780，

擦去的三个数总和：780﹣716＝64，

根据题意，推得擦去的三个数中最小是1，

那么两个质数和63＝61+2能够成立，

61＞39不合题意；

如果擦去的另一个数是最小的合数4，

64﹣4＝60

60＝29+31＝23+37，成立；

综上，擦去的两个质数的和最大是60．

故答案为：39，60．

49．解：边长是9的等边三角形的周长是9×3＝27

第一次“生长”，得到的图形的周长是：27×＝36

第二次“生长”，得到的图形的周长是：36×＝48

第三次“生长”，得到的图形的周长是：48×＝64

第四次“生长”，得到的图形的周长是：64×＝＝85

答：经过两次“生长”操作，得到的图形的周长是48，经过四次“生长”操作得到的图形的周长是85．

故答案为：48，85．

50．解：由图可知，阴影部分的面积是图中最大圆面积的，非阴影部分的面积是图中最大圆面积的，

所以图中阴影部分面积与非阴影部分面积之比是：：＝1：3；

答：图中阴影部分面积与非阴影部分面积之比是1：3．

故答案为：1：3．

以上是小学六年级数学数的认识知识点归纳的相关内容，希望对你有所帮助。另外，今天的内容就分享到这里了，想要了解更多的朋友可以多多关注本站。